| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | |||||
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 17 | 18 | 19 | 20 | 21 | 22 | 23 |
| 24 | 25 | 26 | 27 | 28 | 29 | 30 |
- 백엔드
- 빠르게 실패하기
- 결정트리
- SQL
- 데이터 프로젝트
- sorted
- 비지도학습
- layer normalization
- Batch Normalization
- nvl2
- 오차 행렬
- 평가 지표
- NVL
- 강화학습
- NULLIF
- five lines challenge
- ifnull
- 데이터 분석
- recall
- 웹서비스 기획
- 감정은 습관이다
- beautifulsoup
- 재현율
- LAG
- CASE WHEN
- Normalization
- 지도학습
- 데이터 전처리
- 정밀도
- DecisionTree
- Today
- Total
Day to_day
[선형대수학] 선형성(Linearity)의 조건 본문
❗본 포스팅은 한양대학교 이상화 교수님의 '선형대수' 강의를 기반으로 개인적인 정리 목적 하에 재구성하여 작성된 글입니다.
선형성의 조건 (Linearity)
다음의 조건을 만족하는 것들을 선형성이 있다고 이야기한다.
1. 중첩의 원리 (Superposition) : f(x1 + x2) = f(x1) + f(x2)
개별 요소의 연산 결과를 합한 것이 개별 요소를 합한 후 연산한 결과와 같은 것.
2. Homogeneity : f(ax) = af(x)
상수 a가 있을 때, ax를 input으로 하는 f(x)의 결과나 f(x)의 결과 후에 상수 a를 곱하는 것과 같은 결과를 얻는 것.
두 가지 성질을 만족하는 식을 예를 들어 $y = mx$라는 f(x)가 있을 때,
$m(a_1x_1 + a_2x_2) = a_1mx_1+a_2mx_2 = a_1f(x_1)+ a_2f(x_2)$로 바꿔볼 수 있다.
이것을 도형적으로 봤을 때 원점을 통과하는 직선일 때 linearity를 결정하는 중요한 조건이 된다.
y = mx+n 이런 함수는 실제로 직선으로 그려지기 때문에 linear 할 것 같아 보이지만 위와 같은 방법으로 계산해 보면 linear 하지 않는다. (평면도 마찬가지로 원점을 지나야 한다.)
Linearity 성립하는 행렬

Linearity의 예시를 행렬로 들어 볼 수 있다.
Matrix A와 벡터 X, Y가 있을 때, A라는 matrix와 X의 벡터로 Y벡터를 얻었다면 linear 했는지 알아볼 수 있다.
벡터 X가 [x1, x2]라고 하고, 상수 a1, a2가 있을 때 아래의 수식을 만족시키면 linearity 하다고 할 수 있다.
$$ A(a_1x_1 + a_2x_2) = a_1Ax_1 + a_2Ax_2 $$
선형대수학을 공부하기 위해 알고 가야 할 개념들
행렬 (Matrix)
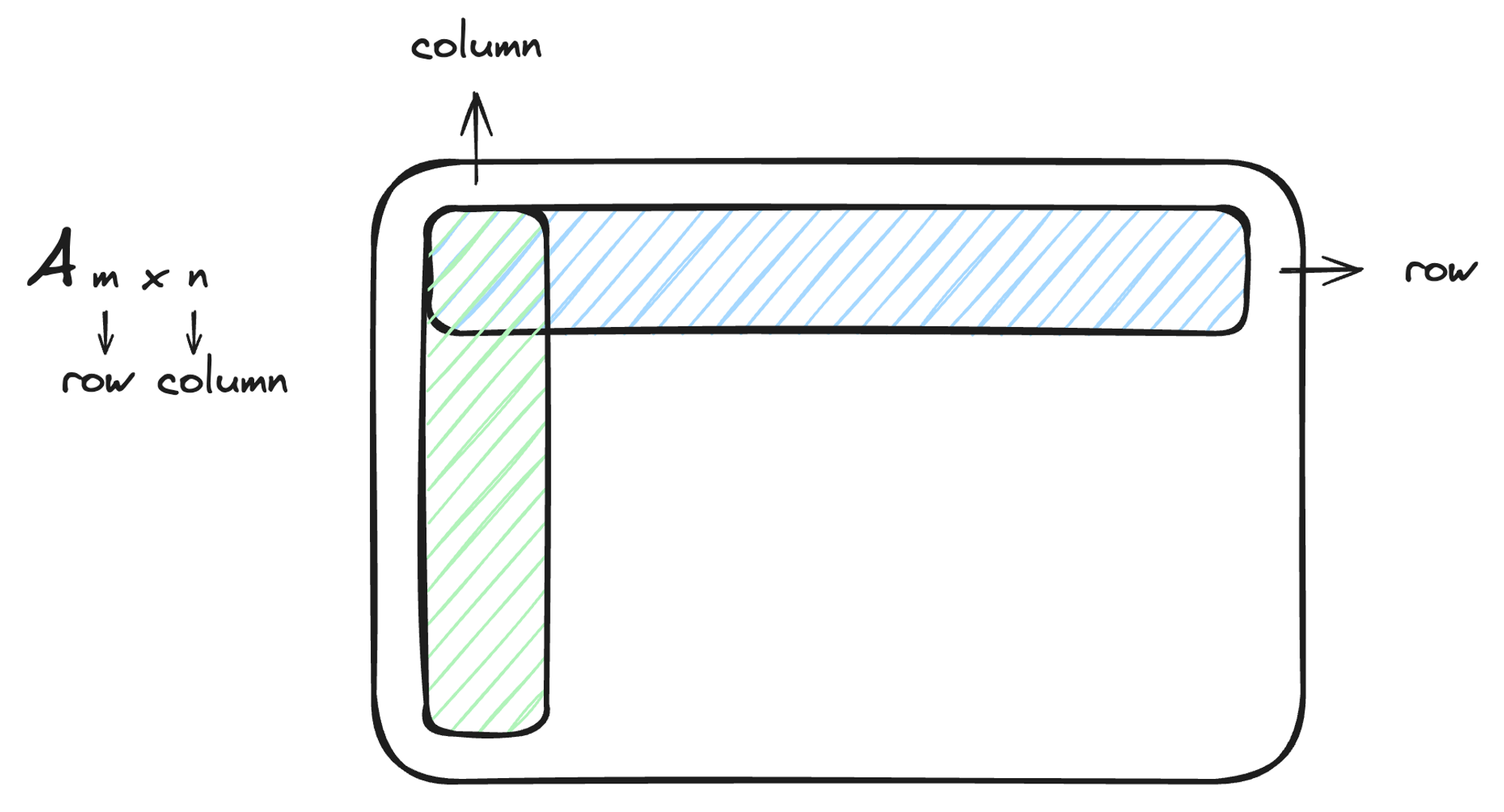
행렬 A가 있을 때 A의 크기를 mxn으로 표현한다면 m은 행의 개수, n은 열의 개수를 의미한다. 행(row)과 열(column)은 위의 그림과 같이 이루어져 있다.
대각 행렬 (Identity Matrix)
대각 행렬은 대각선에 해당하는 값만 1이고 나머지는 0으로 채워진 행렬을 의미하고 $\mathbf{I}$로 표기한다.
$$ \begin{bmatrix}1 & 0 & 0 \\0 & 1& 0 \\0 & 0 & 1 \\\end{bmatrix} $$
보통 행렬은 교환법칙이 성립되지 않는데 대각 행렬은 교환법칙이 성립한다. $\mathbf{IA} = \mathbf{AI}$
역행렬 (Inverse Matrix)
역행렬은 행렬 A와 곱해졌을 때 indentity Matrix가 되는 것을 의미한다.
역행렬이 존재하면 교환법칙이 성립하기도 한다. (”하기도 한다.”라고 이야기한 것은 성립하지 않는 경우도 있기 때문이다 자세한 내용은 다음에 나누어 보겠다)
$$ A^{-1}A = AA^{-1}=I $$
일반적으로 역행렬이 존재하려면 일단 정사각행렬(m x m 행렬)이어야 하고, 하나의 유니크한 값으로 역행렬이 존재한다. 그러나 정사각행렬이라고 해서 모두 역행렬이 있는 것은 아니다.
고등학교 때 배웠던 역행렬을 구하는 공식은 아래와 같이 구했다.
$$ A = \begin{bmatrix} a & b \\ c & d \\ \end{bmatrix} $$
$$ A^{-1}=\frac{1}{ad-bc}\begin{bmatrix} d & -b \\ -c & a \\ \end{bmatrix} $$
선형 결합 (Linear Combination)
벡터의 선형 결합에 대한 기본 개념만 짚고 앞으로 계속 사용할 것이기 때문에 알아두고 넘어가는게 좋다.
만약 벡터 V와 벡터 W가 다음과 같이 있다고 하자.
$$ \mathbf{V} = \begin{bmatrix} a_1 \\ b_1 \\ c_1 \\ \end{bmatrix} $$
$$ \mathbf{W} = \begin{bmatrix} a_2 \\ b_2 \\ c_2 \\ \end{bmatrix} $$
$$ \alpha \mathbf{V} + \beta \mathbf{W} = \alpha \begin{bmatrix} a_1 \\ b_1 \\ c_1 \\ \end{bmatrix} + \beta \begin{bmatrix} a_2 \\ b_2 \\ c_2 \\ \end{bmatrix} =\begin{bmatrix} \alpha a_1 + \beta a_2\\ \alpha b_1 + \beta b_2 \\ \alpha c_1 + \beta c_2 \\ \end{bmatrix} $$
상수 $\alpha$, $\beta$에 대해서 곱하고 더하는 과정을 표현하면 아래와 같이 표현할 수 있다.
그러면 같은 과정을 V와 W를 칼럼 벡터로 넣은 행렬로 만들어서 다음과 같이 표현할 수 있다.
$$ \begin{bmatrix} V & W \\ \end{bmatrix} \begin{bmatrix} \alpha \\ \beta \\ \end{bmatrix} =\begin{bmatrix} \alpha a_1 + \beta a_2\\ \alpha b_1 + \beta b_2 \\ \alpha c_1 + \beta c_2 \\ \end{bmatrix} = \alpha \begin{bmatrix} a_1 \\ b_1 \\ c_1 \\ \end{bmatrix} + \beta \begin{bmatrix} a_2 \\ b_2 \\ c_2 \\ \end{bmatrix} $$
정리하자면 칼럼 벡터 V, W들이 alpha, beta 계수들의 선형조합으로 이루어진다.
여기서 벡터들의 선형 결합은 행렬과 변환이 될 수 있다는 것을 기억하고 넘어가자.
'선형대수학' 카테고리의 다른 글
| [선형대수학] Null space와 Span (4) | 2024.10.09 |
|---|---|
| [선형대수학] 역행렬(Inverse)과 전치 행렬(Transpose) (0) | 2024.09.13 |
| [선형대수학] LU Decomposition (LU Factorization) (0) | 2024.09.03 |
| [선형대수학] 가우스 소거법 (Gaussian elimination) (0) | 2024.09.02 |





