| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 |
- 강화학습
- 비지도학습
- 지도학습
- 재현율
- NULLIF
- 데이터 분석
- layer normalization
- SQL
- sorted
- 결정트리
- Batch Normalization
- DecisionTree
- ifnull
- 데이터 프로젝트
- 데이터 전처리
- CASE WHEN
- 웹서비스 기획
- Normalization
- recall
- beautifulsoup
- NVL
- 정밀도
- nvl2
- five lines challenge
- 평가 지표
- 감정은 습관이다
- 백엔드
- 빠르게 실패하기
- 오차 행렬
- LAG
- Today
- Total
Day to_day
[영상 처리] 카메라 캘리브레이션 (Camera Calibration) 본문
❗본 포스팅은 다크프로그래머의 '카메라 캘리브레이션'과 '좌표계' 포스팅을 기반으로 개인적인 정리 목적 하에 재구성하여 작성된 글입니다.
포스팅 개요
컴퓨터 비전 분야에서 꼭 필요한 기본적인 내용이 카메라 캘리브레이션에 대한 내용이다.
직접 카메라 캘리브레이션을 코드를 짜보며 그 결과를 얻어 카메라 내부 파라미터와 외부 파라미터는 어떤 것인지에 대해서 알아보고자 한다.
일단 카메라 캘리브레이션을 하는 목적을 알기 전에 기본적으로 알고 넘어가면 좋을 좌표계의 개념과 좌표계 변환에 대한 이론을 정리하고 카메라 캘리브레이션에 대해 알아보겠다.
좌표계
우리가 카메라로 어떤 영상을 촬영하면, 카메라 영상은 3차원 공간상의 점들을 2차원 이미지 평면에 투사함으로써 얻어진다. 그때 알아야 하는 좌표계는 다음과 같다.

3차원 좌표계는 카메라 좌표계, 월드 좌표계가 있다.
먼저 월드 좌표계는 실제 사물의 위치를 표현할 때 기준으로 삼는 좌표계이다. 이 좌표계의 특징은 문제에 따라서 우리가 임의로 잡아서 사용할 수 있는 좌표계라는 것이다.
그리고 카메라 좌표계는 카메라를 기준으로 한 좌표계로 카메라의 초점(렌즈의 중심)을 원점, 카메라의 정면 광학축 방향을 Z 축, 카메라 아래쪽 방향을 Y축, 오른쪽 방향을 X축으로 잡는다.
2차원 좌표계로는 픽셀 좌표계와 정규 좌표계가 있다.
픽셀 좌표계는 우리가 실제 눈으로 보는 이미지에 대한 좌표계로서 이미지의 왼쪽 상단 모서리를 원점으로 삼는다. 오른쪽 방향을 x축 증가 방향, 아래쪽을 y축 증가 방향으로 한다.
정규 좌표계는 Normalized image plane이라고 하며, 편의상 도입된 가상의 좌표계이다. 카메라 내부 파라미터 영향을 제거한 이미지 좌표계로 카메라 초점과의 거리가 1인 가상의 이미지 평면을 정의하는 좌표계이다.
좌표계 변환
그렇다면 우리가 실제 보이는 사물의 좌표계에서 2D인 픽셀 좌표계로 바뀌었을 때 좌표를 알고자 할 때 어떻게 변환시켜야 할까?
아래 그림의 과정을 통해 좌표계를 변환시킬 수 있다. 자세히 변환에 대해서 설명하기 전에 여기서 보이는 카메라 내부(Intrinsic parameter), 외부 파라미터(Extrinsic parameter)를 먼저 알아보겠다.

카메라 내부 파라미터
카메라/렌즈 시스템의 내부 파라미터
- 초점 거리(focal length) : fx, fy
- 주점(principal point) : cx, cy
- 비대칭계수(skew coefficient) : skew_c = tan$\alpha$
카메라 외부 파라미터
카메라 좌표계와 월드 좌표계 사이의 변환 관계를 설명하는 파라미터이다.
- 회전 (rotation)
- 이동 (translation)
이제 더 자세히 알아보겠다.
카메라 내부 파라미터
초점거리
카메라마다 고유의 초점 거리를 갖고 있으며 mm 단위가 아닌 픽셀 단위로 표현된다

주점
cx, cy는 카메라 렌즈의 중심 즉, 핀홀에서 이미지 센서에 내린 수선의 발의 영상좌표로서 일반적으로 말하는 영상 중심점과는 다른 의미이다.
비대칭 계수 (skew coefficient)
비대칭 계수 skew_c는 이미지 센서의 cell array의 y축이 기울어진 정도를 나타낸다. 그런데 요즘 카메라들은 이러한 skew 에러가 거의 없기 때문에 카메라 모델에서 보통 비대칭 계수까지는 고려하지 않는다고 한다. (즉, skew_c = 0).

카메라 외부 파라미터
카메라 좌표계와 월드 좌표계 사이의 변환 관계를 설명하는 파라미터이다. 두 좌표계 사이의 회전(rotation) 및 평행이동(translation) 변환으로 표현된다.
카메라 외부 파라미터는 카메라 고유의 파라미터가 아니기 때문에 카메라를 어떤 위치에 어떤 방향으로 설치했는지에 따라 달라지고 또한 월드 좌표계를 어떻게 정의했느냐에 따라서 달라진다.
그럼 다시 좌표계 변환으로 돌아와서
외부 파라미터는 카메라 좌표계와 월드 좌표계 사이의 변환 관계를 설명하는 파라미터라고 했다. 그래서 월드좌표계에 외부 파라미터를 곱하면 카메라 좌표계로 변환할 수 있다.
그리고 카메라 좌표계에서 픽셀 좌표계로 변환하기 위해서 다음의 그림을 참고하면 좋다.

- 카메라 좌표계 상의 한 점 (Xc, Yc, Zc)를 영상좌표계로 변환할 때 먼저 Xc, Yc를 Zc(카메라 초점에서의 거리)로 나눠 normalized image plane 상의 좌표로 변환하기 (초점으로부터 거리가 1인 normalized image 평면에 위치한 좌표로 변환가능)
- 여기에 다시 초점거리 f를 곱하면 우리가 원하는 이미지 평면에서의 영상좌표(pixel)가 나온다. 그런데, 이미지에서 픽셀좌표는 이미지의 중심이 아닌 이미지의 좌상단 모서리를 기준(원점)으로 하기 때문에 실제 최종적인 영상좌표는 여기에 (cx, cy)를 더한 값이 된다.
- 즉, x = fxX/Z+cx, y = fyY/Z+cy.
그것을 식으로 정리한 것은 아래와 같다.
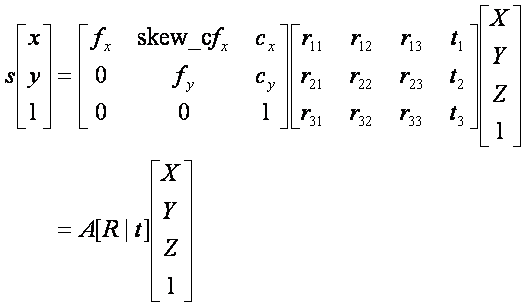
카메라 캘리브레이션 (Camera Calibration)
이제 카메라 캘리브레이션을 통해 카메라 내부, 외부 파라미터를 구할 수 있다.
카메라 캘리브레이션의 flowchart는 아래와 같고, circle grid를 사용하여 코드를 짰다.
캘리브레이션에 사용한 사진은 20장 정도를 넣어주었고, 각도를 약간씩 다르게 하여 촬영했다.

결과
코드는 깃허브 링크를 통해 남겨두겠다.
GitHub - minglet/Image-Processing
Contribute to minglet/Image-Processing development by creating an account on GitHub.
github.com


결과는 다음과 같이 나왔고, intrinsic parameter와 extrinsic parameter를 구했다.
R vector와 T vector는 input 데이터로 넣은 이미지만큼의 벡터가 나오는데 전부를 다 보여주기 어려워 중간에 잘라서 붙여 넣은 것이다. (개수가 맞지 않다고 이상하게 생각하지 말길..)
다음 포스팅
다음엔 캘리브레이션을 통해 얻은 파라미터를 가지고 좌표계 변환해서 pointcloud를 만드는 것에 대한 포스팅을 남기겠다.
'영상처리' 카테고리의 다른 글
| [영상 처리] 2D 좌표에서 3D pointcloud로 변환하기 (0) | 2023.06.03 |
|---|

