| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- DecisionTree
- 웹서비스 기획
- 비지도학습
- 강화학습
- Normalization
- five lines challenge
- 데이터 전처리
- NULLIF
- 백엔드
- 지도학습
- sorted
- 데이터 프로젝트
- SQL
- beautifulsoup
- 결정트리
- 재현율
- recall
- 정밀도
- nvl2
- 오차 행렬
- ifnull
- LAG
- CASE WHEN
- NVL
- 감정은 습관이다
- 평가 지표
- Batch Normalization
- 데이터 분석
- 빠르게 실패하기
- layer normalization
- Today
- Total
Day to_day
[지도 학습] 규제 선형 회귀 L1, L2 norm (Ridge, Lasso, ElasticNet) 본문
[지도 학습] 규제 선형 회귀 L1, L2 norm (Ridge, Lasso, ElasticNet)
m_inglet 2023. 6. 16. 17:17포스팅 개요
규제선형회귀란 무엇이고, 먼저 알고 넘어가야 할 개념인 L1 norm과 L2 norm을 살펴보겠다.
그리고 규제선형회귀인 릿지 회귀, 라쏘 회귀 그리고 ElasticNet에 대해서 알아보는 포스팅이다.
규제 선형 회귀

이전엔 오차만 줄어들면 장땡이었는데, 이젠 오버피팅 문제 때문에 회귀 모델이 적절하게 적합하면서 회귀계수가 너무 커지는 것을 제어해야 한다. 그래서 규제 선형회귀는 이것을 목적으로 한다. 이전엔 Loss값인 RSS만 최소화하였는데 규제 선형회귀에서의 목표는 다음과 같다.

이때 alpha의 역할은 이 중요하다.
alpha가 0에 가까우면 이전 식(Min(RSS(W))과 같아진다.
또 alpha가 너무 커지면 W값이 작아지는 목표를 갖고 비용함수가 만들어져야한다.
즉 alpha 값을 크게 하면 비용함수는 회귀 계수 W의 값을 작게 해 과적합을 개선할 수 있으며 alpha 값을 작게 하면 회귀 계수 W의 값이 커져도 어느 정도 상쇄가 가능하므로 학습데이터 적합을 더 개선할 수 있다.
다시 정리하자면,
- alpha 감소 → RSS(W) 최소화
- alpha 증가 → 회귀 계수 W 감소
- alpha = 0 : W가 커도 alpha*||W||^2가 0이 되어 비용함수는 Min(RSS(W))
- alpha = 무한대 : alpha*||W||^2도 무한대가 되므로 비용함수는 W를 0에 가깝게 최소화해야함
규제 선형회귀의 유형에 대해서 알아보기 전에 일단 L1 norm과 L2 norm의 개념에 대해 알고 넘어가면 좋겠다.
L1 norm
Norm은 벡터의 크기를 측정하는 방법이고, 두 벡터 사이의 거리를 측정하는 방법이다.
L1 norm은 맨해튼 거리라고 알려져 있으며, 택시가 도시의 블록 사이를 이동해 목표 지점까지 이동하는 것과 같이 표현한다.
목표 지점까지 도달하는 방법은 여러 가지가 있을 수 있으며 그중에서 최단 거리를 찾는다.

L1 loss function은 실제 값과 예측 값 오차들의 절대 값들에 대한 합이다.
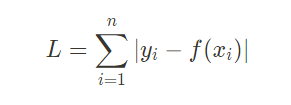
L2 norm
L2 norm은 유클리드 거리라고도 하며, 두 점 사이의 최단 거리를 측정할 때 사용된다.
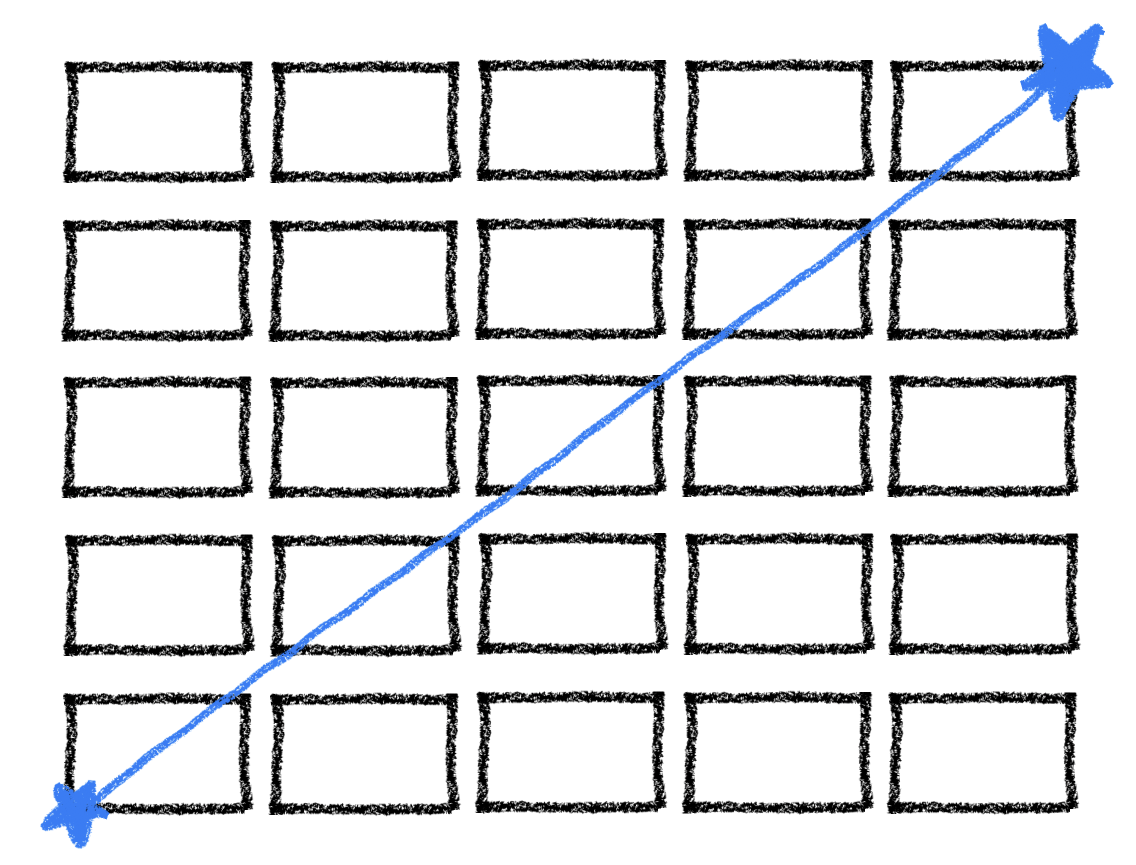
L2 loss function은 실제값과 예측값 사이의 오차를 제곱한 값들의 합이다.

릿지 회귀 (Ridge) : L2 규제
너무 많은 독립 변수를 갖는 모델에 페널티를 부과하는 방식으로 기존 선형 회귀의 과적합을 방지한다.
그래서 일반적인 선형회귀에서는 MSE(평균제곱오차)가 최소가 되는 것을 계산하지만 규제 회귀분석에서는 MSE에 규제항이 붙어서 MSE + 규제항이 최소가 되는 회귀 계수를 추정한다.
라벨값(y)과 예측값(y^) 사이의 평균제곱오차인 MSE에 규제항으로 L2 항을 추가한 것이 릿지 회귀이다.

모델에 큰 영향이 없는 독립변수의 회귀계수 크기를 0에 가깝게 축소시킨다.
alpha 값을 이용하여 회귀 계수의 크기를 조절
alpha값이 크면 회귀 계수 값이 작아지고, alpha값이 작으면 회귀 계수 값이 커진다.
라쏘 회귀 (Lasso) : L1 규제
- W의 절댓값에 패널티를 부여하는 L1 규제를 선형 회귀에 적용한 것이 라쏘 회귀이다. 이때 L1 규제는 alpha*||W||를 의미하고 라쏘 회귀 비용함수의 목표는 RSS(W) + alpha*||W|| 식을 최소화 하는 W를 찾는 것이다.
- MSE (손실함수)에 α를 곱한 L1규제항을 더한 것이다.

- 학습의 방향이 단순히 손실함수를 줄여나가는 것뿐만 아니라 가중치(W) 값들 또한 최소가 될 수 있도록 진행한다.
- 라쏘도 릿지처럼 계수를 0에 가깝게 만들려고 하는데 라쏘에서 어떤 계수는 정말 0이 된다. 이 말은 모델에서 완전히 제외되는 특성이 생긴다는 뜻이다.
- alpha의 값이 중요한 하이퍼파라미터가 될 텐데, alpha를 높이면 어차피 전체 페널티의 값도 줄여야 하니 가중치의 합도 줄이도록 학습하게 된다. 그렇다면 alpha를 높여 전체 비용함수의 값을 줄이면서 w값도 줄일 수 있다.
- L2 규제가 회귀 계수의 크기를 감소시키는데 반해 L1규제는 불필요한 회귀 계수를 급격하게 감소시켜 0으로 만들고 제거하는 특징이 있다.
- L1 규제는 적절한 피처만 회귀에 포함시키는 feature selection의 특성이 있다.
⇒ 정리하자면,
일반적으로 라쏘(Lasso)는 특성이 0이 되는 것이 많다. 하지만 릿지(Ridge)는 크기가 작아져도 0이 되진 않는다. 실제로 이 두 모델 중 보통을 릿지 회귀를 선호한다. 하지만 특성이 많고 그중 일부분만 중요하다면 라쏘가 더 좋은 선택일 수 있다. 또한 분석하기 쉬운 모델을 원한다면 라쏘가 입력 특성 중 일부만 사용하므로 쉽게 해석할 수 있는 모델을 만들 것이다.
Elastic Net
- L2 + L1 규제 결합한 방법이다.
- 라쏘 회귀가 서로 상관관계가 높은 피처들의 경우에 이들 중에서 중요한 피처만 선택하고 다른 피처들은 모두 회귀계수를 0으로 만드는 성향이 강하다. 그렇기 때문에 특정 피처들에 대한 의존도가 높고 alpha값에 따라 회귀 계수의 값이 급격히 변동할 수도 있다.
- 그래서 L2규제를 포함시키면서 L1규제를 제어해 보자!
Elastic Net 회귀 파라미터
엘라스틱넷 규제는 다음 식과 같이 설명할 수 있다.
a * L1규제 + b * L2규제
L1_ratio 파라미터 값은 a/(a+b)
L1_ratio가 0이면 a = 0 L2 규제와 동일
L1_ratio가 1이면 b = 0 L1 규제와 동일
0 < L1_ratio < 1 이면 L1과 L2 적절히 적용
릿지와 라쏘에 관한 관련 코드는 아래 깃허브에 올려두었습니다!
GitHub - minglet/ML_study
Contribute to minglet/ML_study development by creating an account on GitHub.
github.com
'Machine Learning > 지도 학습' 카테고리의 다른 글
| [지도 학습] 회귀 분석의 목적과 종류 (0) | 2023.05.07 |
|---|---|
| [지도 학습] 로지스틱 회귀 (Logistic Regression) (1) | 2023.04.22 |
| [지도 학습] 스태킹 모델에 대해서 자세히 알아보기! (구현 코드) (0) | 2023.03.20 |
| [지도 학습] LightGBM 개념과 예제 코드~! (1) | 2023.03.17 |
| [지도 학습] 여러가지 부스팅 알고리즘 알아보기 (GBM, Adaboost, XGBoost) (0) | 2023.03.15 |




